TomTom Rules and Info
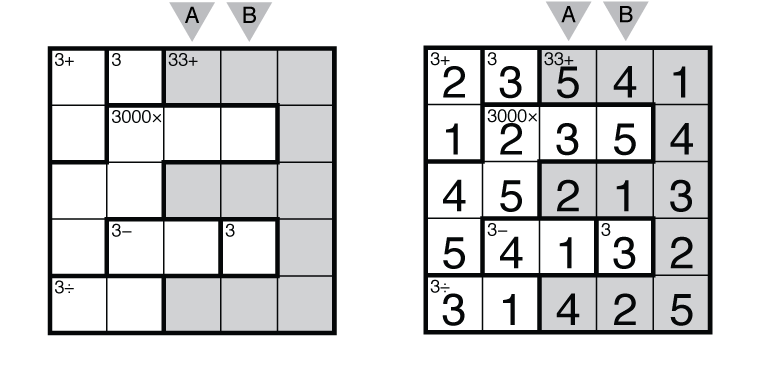
Rules: Insert a number from 1 to N into each cell in the N by N grid so that no number repeats in any row or column. Also, the number in the upper-left corner of each bold cage indicates the value of a mathematical operation (addition, subtraction, multiplication, division) applied successively to all numbers in the cage, starting with the largest number for subtraction and division (e.g. 1,2,4 with subtraction is a 1- clue as 4-2-1 = 1). The operation may or may not be given in the cage, but at least one of the four operations must apply. Numbers can repeat within a cage.
Answer String: Enter the row/column marked “A”, followed by a comma, followed by the row/column marked “B”. Rows are entered from left to right and columns from top to bottom. This example has the key “53214,45132”.
(Brief) History of TomTom: Descended from other Latin Square puzzle types. The style was first broadly created by Tetsuya Miyamoto, a Japanese math teacher looking for new approaches to educating his elementary school students, under the name KenKen (TM of Nextoy). The puzzle came to the west several years after sudoku with similar computer-generation to meet apparent demand, with the noteworthy result of publication in The New York Times where sudoku never appeared. Behind the efforts of Thomas Snyder, the puzzle evolved in numerous ways, including new explorations of symmetry and theming, increased difficulty, varied number ranges, and changes to the rules to better handle subtraction and division. This new evolved puzzle style was named “TomTom” after its main innovator.
History of this example: This puzzle was the first TomTom written for the blog series “Thomas Snyder Outdoes the NYT KenKen”. It was first published on 3/3/09, Square Root Day, one day after a mocking post about how the NYT KenKen had been themed around the number “3”.
Sources for TomTom Puzzles: Follow this link for classic TomTom puzzles on this website and this link for variations on TomTom puzzles. If you are new to this puzzle type, here are our easiest TomTom Puzzles to get started on. More TomTom puzzles can be found in the TomTom collection, in The Art of Puzzles, and in our beginner-friendly collection Intro to GMPuzzles by Serkan Yürekli.
Design rules for contributors: A Grandmaster TomTom will have a unique solution that can be reached by logic alone. Generally, a Grandmaster TomTom should be themed with some combination of symmetry, interesting cage shapes, or interesting clues. Cages may be shaded to help display the visual theme. Not all cages need to be clued. Other number ranges (even using 0 or negative integers) are allowed. Sizes from 5 by 5 to 9 by 9 are recommended.

Hello I recently stumbled across the Union Jack TomTom. After some wrestling I think I solved it but was wondering if I really have done so. I wonder if I am really understanding the constraints. Can a cage that says 1/ be comprised of a 6, 4 and 1 —- such that .6 + .4 = 1 and 1/1 = 1? Can a cage that is labelled 2/ be comprised of 7, 6, 3 and 1 such that 7 + 3=10 and 6-1 = 5 and 10/5 = 2?
No. With your examples you are being too creative and mixing operations. This isn’t an instance of the 24 game where you are looking for some combination of numbers and operations to get a result which (7+3)/(6-1) would be. All you do in the Union Jack is successive application of the same operation for the target set of integers starting from the largest value. 1/ could be 1,2,3,6 because 6/3/2/1 = 1. Similarly 2- could be 1,2,5 as 5-2-1 = 2.