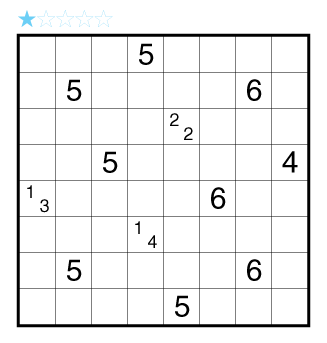
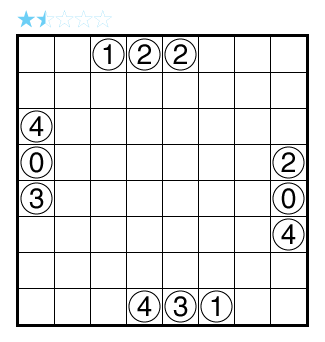
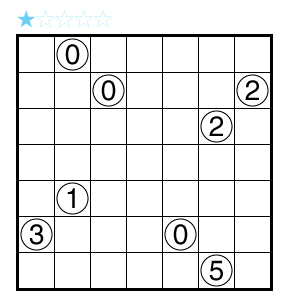
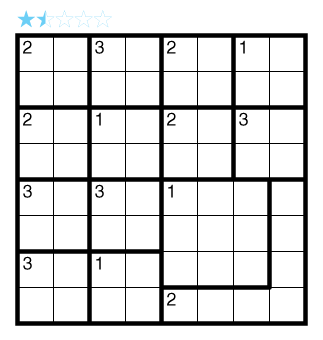
Aqre (Symmetry) by Serkan Yürekli
This is a free “warm-up” puzzle; Season 4 subscribers will see today’s main puzzle in the same style posted at 9:05 AM PT.
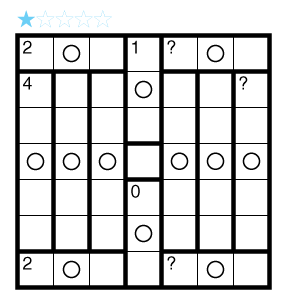
or solve online (using our beta test of Penpa-Edit tools; use tab to shift between shading mode and the composite Yajilin mode where left click marks cells, right click marks dots in cells or X’s on edges, left click+drag draws lines.)
Theme: Into the Unknown
Author/Opus: This is the 506th puzzle from our managing editor Serkan Yürekli.
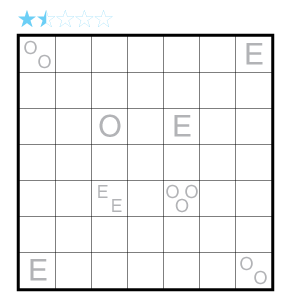
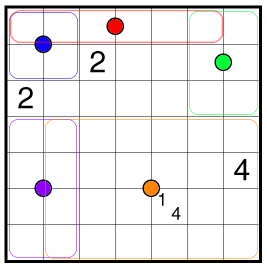
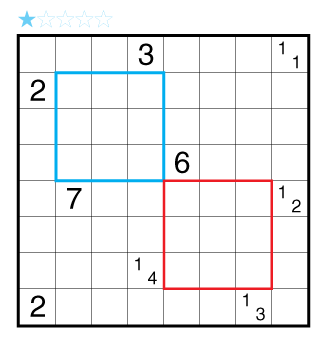
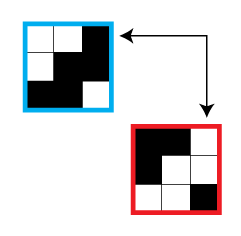
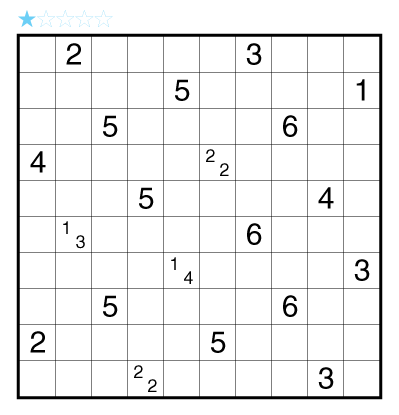
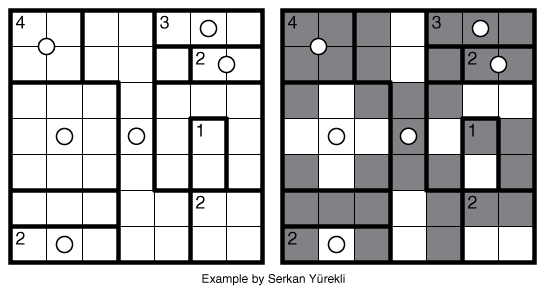
Rules: Standard Aqre rules. Also, some regions have a circle in their center. In these regions, the shaded cells must have 180° rotational symmetry around the circle of the region. There is no restriction on regions without a circle. A ? can represent any Aqre number clue, including zero.
Difficulty: 1 star
Time Standards (highlight to view): Grandmaster = 0:40, Master = 0:50, Expert = 1:40
Solution: PDF and solving animation.
Note: Follow this link for more Aqre puzzles. If you are new to this puzzle type, here are our easiest Aqre to get started on. More Aqre puzzles can be found in these books in our e-store.
Note 2: Comments on the blog are great! For a more interactive discussion, please also consider using our Week 12 Discussion post on the GMPuzzles Discord.