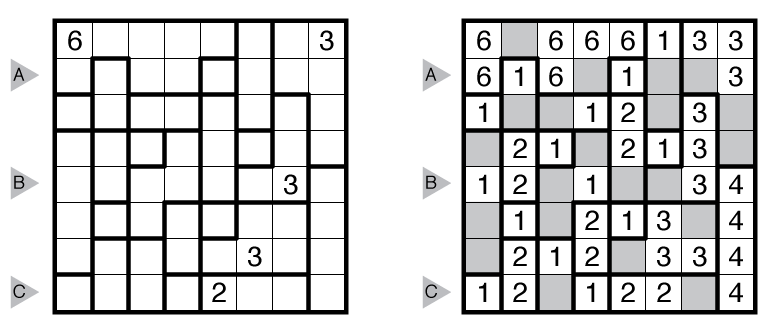
Rules: Label some cells with numbers to form a single connected group of labeled cells; no 2×2 group of cells may be fully labeled. Each bold region must contain at least one labeled cell. Each number (including any given numbers) must equal the total count of labeled cells in that region. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. (Note: While not required, it may be helpful to shade in the unused cells, as seen in the solution here.)

Answer String: Enter the length in cells of each of the segments labeled with numbers from left to right for the marked rows, starting at the top. Separate each row’s entry with a comma. This example has the key “311,212,231”

(Brief) History of Nanro: Nanro was first published in 2000 by Nikoli in quarterly Communication 92; the original author of the style was nyoroppyi (Yuki Kawabe).

History of this example: This example was written for the instruction booklet of the LMI Puzzle Marathon in 2013.

Sources for Nanro Puzzles: Follow this link for Nanro puzzles on this website and this link for variations on Nanro puzzles. If you are new to this puzzle type, here are our easiest Nanro Puzzles to get started on. More Nanro puzzles can be found in A Number o’ Nanro by Prasanna Seshadri.

Design rules for contributors: A Grandmaster Nanro will have a unique solution that can be reached by logic alone. Generally, a Grandmaster Nanro will have symmetric clues, symmetric regions, or an interesting pattern of regions in the absence of symmetry. Sizes from 8×8 and above are recommended (maximum aspect ratio of 2:1 if rectangular).