From the Foxger’s Den #55: Pentominous
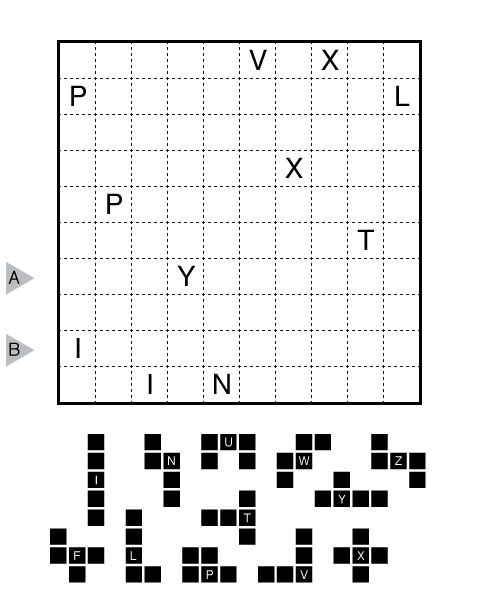
or solve online (using our beta test of Penpa-Edit tools; use tab to alternate between a composite mode for line/edge drawing and a letter entry mode.)
This is a “Twisted Tuesday” puzzle variation.
Theme: Logical
Rules: Variation of Fillomino rules where regions with the same shape must avoid each other instead of regions with the same size (all regions in a pentominous puzzle are pentominoes).
Specifically, divide the grid into 20 pentominoes so that no two pentominoes of the same shape (including rotations/reflections) share an edge. A cell with a letter in it must be part of the pentomino shape normally associated with that letter as given below the grid. Not all pentomino shapes need appear.
Answer String: Enter the letter associated with the pentomino occupying each cell in the two marked rows from left to right, separating the rows with a comma. Use CAPITAL LETTERS!
Time Standards (highlight to view): Grandmaster = 2:00, Master = 4:30, Expert = 9:00
Solution: PDF
Note: Follow this link for other puzzles involving Pentominoes.

Nice concept for a variant, but I didn’t spot the logic of the bottom-right corner and ended up doing a little trial and error to make it work. I get it involves placing some of the Y and N blocks with certainty, and then I guess it’s figuring out how to divide the rest in order to avoid duplication (Two P pentominoes in particular?).
I testsolved this puzzle (personally by mathgrant 😛 ) and I also used trial and error at that corner. But now I solved it again, there seems to be a very narrow logical step: Try seeing what ahppens with R5C5. There’s a lot of what-if’s, but none goes more than putting two or three pentominoes.
My logic was as follows:
1. R6C4 can’t be joined with R5C5 as it would form either a F, X or Y, all of which it would already be touching. So it’s part of the Y, which will then go vertical.
2. R10C4 is now part of the N and so are R9C67.
3. The right bottom corner now has 9 cells that can’t be part of the N and have only one exit point, which means that either R10C6 or R8C8 forms 2 pentominos with those 9 cells.
4. R7C8 is thus part the second pentomino in the middle as it can’t reach R5C5.
5. R9C5 needs to join with N as it can’t reach R7C8 and this is the only pentomino it can now be part of.
Now you can figure out how to fill the rest pretty simply.
I hope this is clear.
Nice and easy
Friendly start with a slightly tricky finish. Very nice.
Puzzle link [EDIT: Removed as we added our own official link to post]
4.30 Mins to solve this one. It was tricky to find correct placements in the lower right corner.