Championship Chatter – How Many Roads …?
I received a lot of “pre-criticism” about having made a Counting Puzzle for the USPC. I have been rather outstated as a solver in not liking these puzzles because of the difficulty of confirming one’s answer — particularly in the old -5 point days for a mistake that would frequently cost me for even attempting and getting close to the right answer. And I often don’t get the choice to skip it when I’m close to finishing the test.
But that doesn’t mean I’ve never been called on to write Counting Puzzles. I wrote a GAMES article/Puzzlecraft chapter on the topic. And I gave it another attempt on this USPC. Call it an experiment to see if I could make anything my audience would accept as a good puzzle.
My first concept was to make a heavy path puzzle with lots of forced segments due to arrows, but not a single solution to give it a “counting” aspect. While I figured good solvers would be able to get to a “trivial” state to count a handful of total paths, all of my initial designs ended up feeling more like a broken path puzzle than a good counting puzzle so a changed goals slightly. I wondered: can I make a few very simple counting challenges work together with some simple math to be a fair challenge. Basically, something where good observation could reduce the problem into something much more tractable. And if this is testing both observation and problem solving skills in an unfamiliar setting, all the better.
Even with the “simple” format below that even had the surprise of very basic multiplication built in, the successful answer rate was quite low compared to my own expectations. And at least one solver has complained about getting 99.991% of the correct answer and getting zero credit. In my evaluation, with three small counting puzzles and a meta puzzle of building the math equation, that answer is 75% correct in the same way some of the answers in the 52k range were. All from counting one of the component puzzles one lower than expected.
So, did you think this was an appropriate USPC challenge? Did this soften or strengthen opinions against counting puzzles? Are counting puzzles still the brussel sprouts of the USPC buffet? I’ve only heard positives from people that actually got the puzzle correct so I do have to think score results often bias counting puzzle reviews (my strongly negative reviews have certainly followed my average score of -5 on these puzzles over the years).
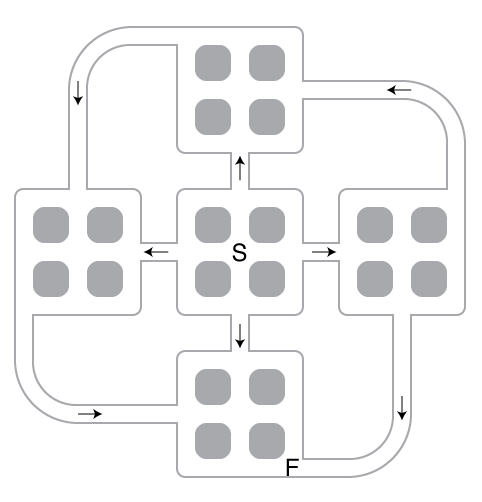
Theme: Symmetry, mainly
Rules: Count the number of different paths from Start (S) to Finish (F). You cannot use an intersection or a path segment more than once. Path segments with arrows can only be used in the indicated direction.
Answer String: For the USPC, the answer string was the number of paths. For this week, you can just hit the solved button on an honor system if you think you’ve solved it.
Solution: PDF
And if you want an extra challenge, solve this bonus puzzle where an arrow has been removed. It’s one step up from the original puzzle but should be just as simple to break into constituent parts if you’ve mastered the first.

Well, I did skip this one during the test, but I probably shouldn’t have. This is definitely a better form of counting question. For one thing, it’s a “math-ier” form of counting question, really more the sort of thing that appears on math competitions (which is why Palmer astutely linked an AMC problem in his pre-competition notes). Also, when it comes right down to it, the individual “counting” portions really only boil down to three basic situations you need to count, which have 7, 10, and 8 possibilities each, and are therefore very manageable. Plus, the puzzle is arranged so that the arithmetic in adding it all up is easy. I’d say it’s fair, and I sort of wish I’d done it during the test (which I’ve never said about a counting puzzle before).
I thought this was a good counting/math puzzle. I also prefer to score positive points for the puzzles I solve, but I might have tried this one during the test if the timing toward the end had been different.
I like the idea of the puzzle itself, but the rules I thought were unclear, especially for this type of puzzle that doesn’t have any sort of example in the instructions. I didn’t participate in the USPC officially but I would’ve answered “3” (the maximum number of possible paths if no segment is re-used, period).
I was just embarrassed that even with a doctorate in maths, the time pressure caused me to slip up on this one.
I like the puzzle, and it sounds like it was appreciated by the maths fans. I personally think it needs a vague hint such as “The digits of the answer sum to 30”. Then people can spend as long as they like on it if they so choose, searching for a valid solution, rather than having a good guess and moving on?
Also, counting puzzles are better suited to the instant-marking systems that LMI sometimes uses.
I helped create instant marking for just this sort of situation. I’m sad it isn’t used in more places or more often at LMI, but I can understand why the USPC prefers the standard system given how careful the organizers treat regrading and protests given potential answer key mistakes with so many different puzzle styles.
“And at least one solver has complained about getting 99.991% of the correct answer and getting zero credit.”
I actually missed that the rightmost square was an edge to edge case with only 8 possible paths and thought it was the same edge to corner case, so ended up computing 70+70+700+7000+70000 = 77840. I don’t begrudge the points at all, though, since it really means that I messed up 1 of the 5 “cases”.
I did like the puzzle, though.
I didn’t have too much trouble with this one, even though I did under count the number of paths at first glance (it was quickly fixed though). In fact, compared to the other puzzles, this one wasn’t hard.
@James: Isn’t mathematicians supposed to suck at counting/arithmetic, and only good at advanced mathematics? That’s my impression at least (I am allowed to make such a joke since I am a math grad student myself.)
Good point Aaron, after high school there are hardly any numeric calculations in maths. Maybe this puzzle suits accountants more? 😉
I thought it was a fine puzzle. I would criticize it a bit for being too mathy and not puzzly enough, and I would criticize me for bungling the counting in a particularly ridiculous way, mostly by seeing how mathy it was and rushing through it instead of checking carefully as I might have in a more puzzly counting problem.
I spend significant amounts of my time teaching kids how to solve puzzles like this, so it’s rather embarrassing to have missed this one.