Ask Dr. Sudoku #14 – Thinking in Groups
I knew when constructing puzzles for this past week that it would end up pretty tough across the board. I had certain themes in mind and when constructing for a particular goal you cannot always tailor the timing precisely. I believe — except for Monday’s puzzle — everything was rated for at least 5 minutes. It is probably asking too much to expect a full week to “feel perfectly balanced” when there are six different styles being presented.
So, while it may be impossible to avoid “hard” weeks in the future, this did seem an apt time to return to discussing some of these puzzles. I got a specific request to describe Saturday’s Battleships in logical terms, so that is what I’ll cover today.
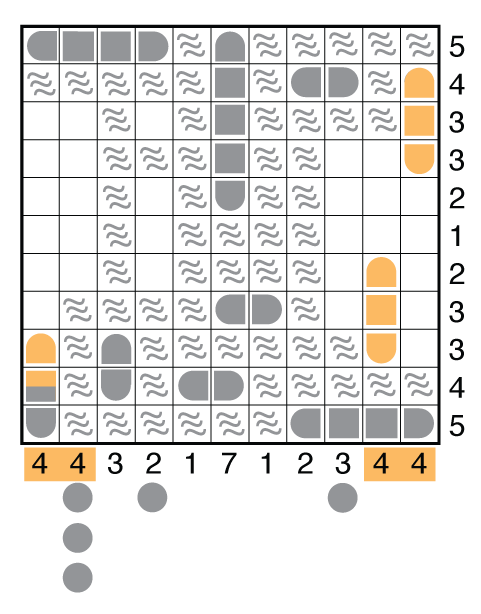
The key to this puzzle, at different times, is to really think in groups. Many Battleships puzzles involve just thinking about the 4-unit battleship first. But a very small number require you to consider both the 4-unit battleship and 3-unit cruisers together. This puzzle is like those, except the fleet has grown super-sized.
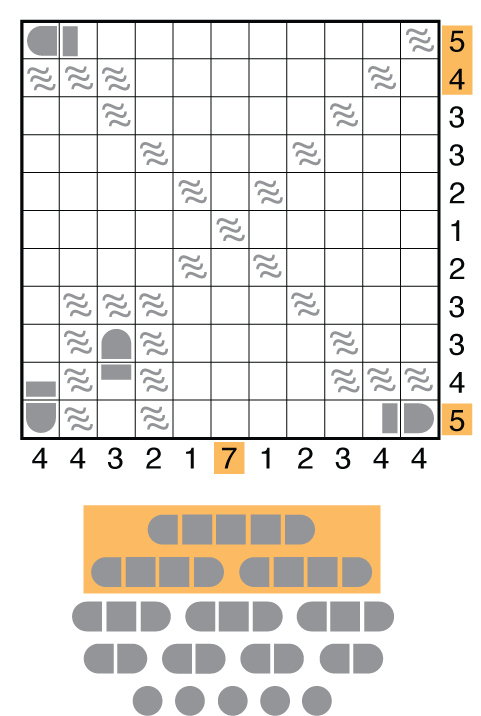
There are 3 very big ships in this puzzle but only 4 rows or columns (in orange) that can take any of them. Note that no row/column can have two so exactly three of these four will be used. Normally this doesn’t say too much in a puzzle, but whenever the big rows are next to each other (as in R1 and R2), you will most often find that you cannot use both of them simultaneously. The break-in to this puzzle is to mentally sort out that this is the case. Consider the following:
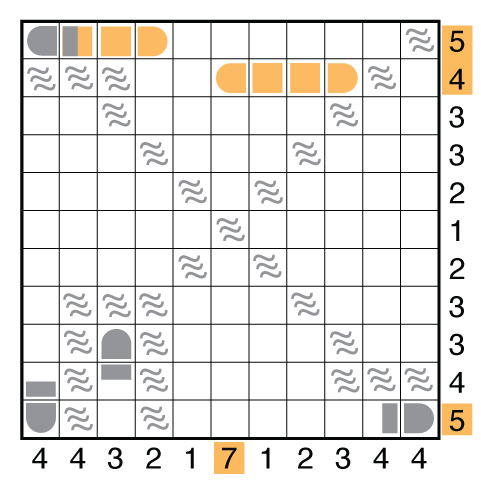
This is the only way to place two big ships in each of the first two rows. But you cannot complete the first row to get to five segments. So only one of the top two rows has a big ship, as well as C6 and R11.
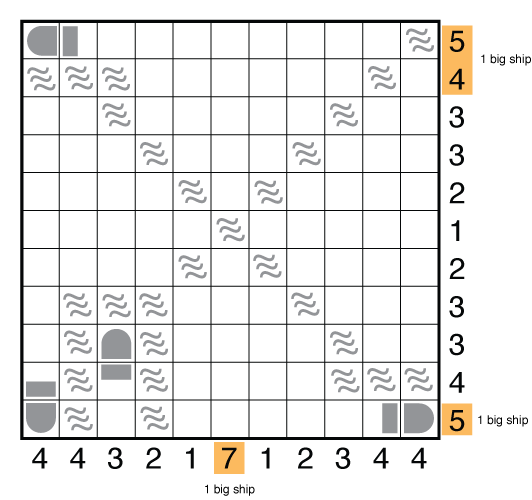
So start at the bottom row and fill in all consequences from it containing a 4-unit ship. Just as we saw a problem with the 54 rows at the top containing large ships, once the 4-unit ship is in the bottom row, the row just above that is very limited now to just one option. Progress takes you to here.
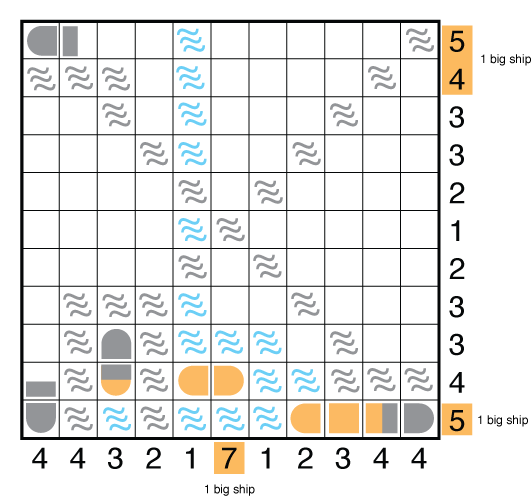
Reconsider the big ships. In isolation, the center column must take at least 3 ship segments in rows 2/3/4 whichever of the 4-unit or 5-unit ships goes there. But really you can use all the eliminations made by seas (if you got them in the grid) to recognize there is just 1 place left for the 5-unit ship which gets you all the way to the second image below.
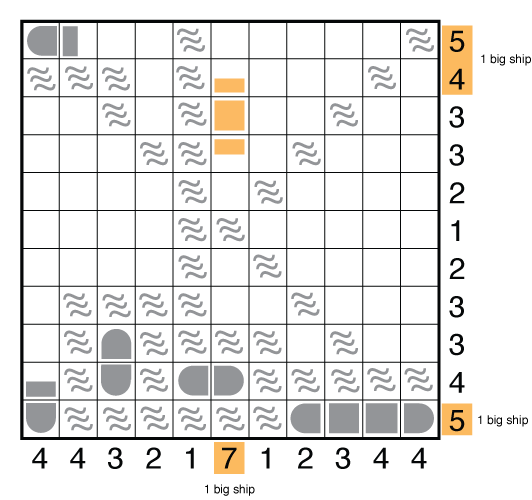
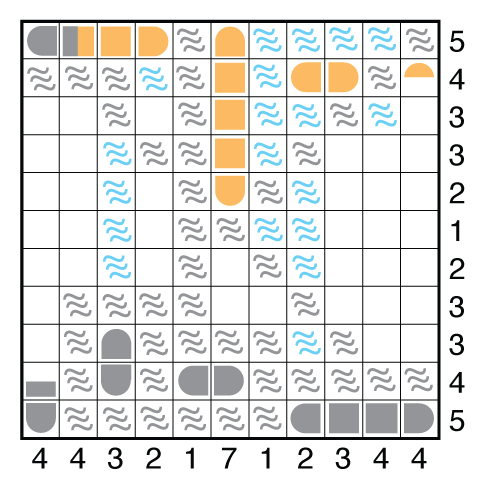
Filling in the remaining consequences of fitting in these big ships should place you at this stall point roughly. This is where fleet bookkeeping comes back into play. Notice that there are only 1-unit and 3-unit ships left to place.
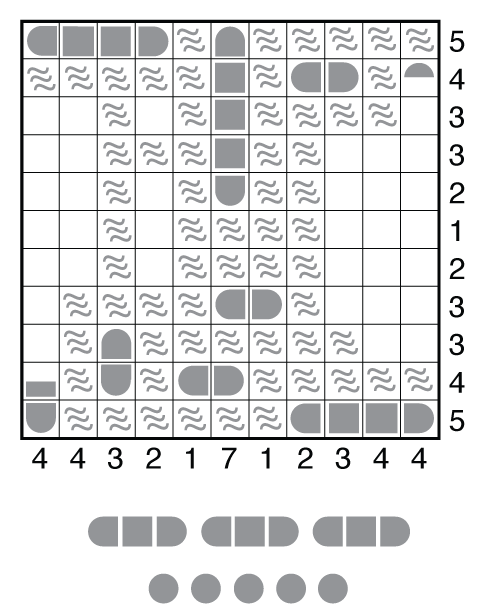
Further, notice that none of the 3-unit ships can be placed horizontally. There are only 4 columns in which they can go, and again only 3 of these 4 columns will be used. The question is which 3 of 4.
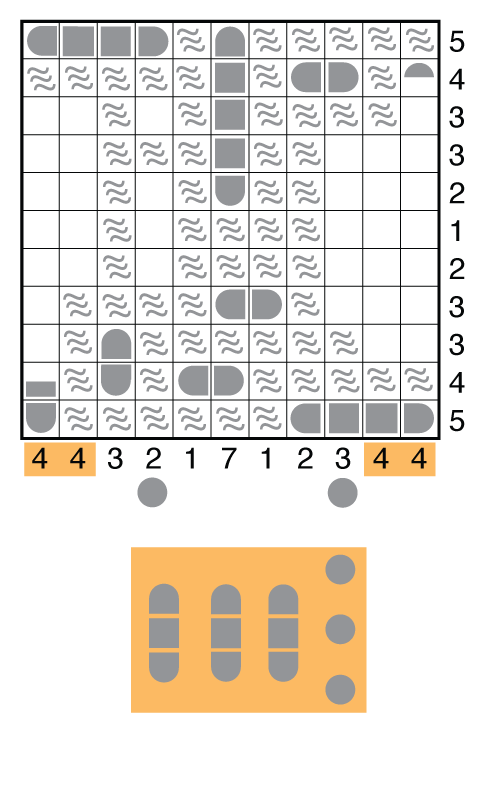
Column 1, from the given clue, is a certainty. Columns 2, 10, and 11 are less sure. Notice that whichever column does not get a vertical 3-unit cruiser is getting 3 submarines. These will cancel a much larger number of positions in the adjacent column. Again, consider what this means when you have two big numbers left to fill in adjacent columns. You should recognize there is no way the 3 subs can fit into C10 or C11 then to leave a way to fill the other column. So you can deduce this is the only set of positions for the 3-unit ships, and from there place the remaining submarines quickly to finish off the puzzle.
You may ask — well, how can you know when to consider ships individually and when as groups when thinking about placements. As with all heuristics, there is no sure way to know when this one will work and others you could try won’t. My opinion on what separates the best solvers (top 10 in world) from the next group (top 100+) is not knowing the heuristics, but not wasting time trying the less likely ones that will succeed at a particular time. So experience is important here. What cues exist in this puzzle?
Well, this puzzle has a lot of effectively small numbers as a result of having no 0 outside clues. There are only 3 outside clues that could indicate a 5-unit ship but only 2 are effectively possible with the interior clues. Once you start considering these effective sizes, you’ll notice that there aren’t many spots for 4’s either because of how the symmetric clues in R1C1, R11C1, and R11C11 work together. A second tell-tale sign that almost always is the source of constraints in battleships is when big numbers sit next to each other. Since ships cancel neighboring cells, your eye needs to get used to recognizing why it is valuable to test R1 and R2 immediately to cancel one of them from having a big ship. Combining observations not just on how many rows can fit bigger ships, but also where these rows sit in relation to each other, will certainly help improve your battleships “logical” solving capacity.

The commentary about timing has me thinking. If you ever do add the ability to report times with solutions, would it be possible to add whether it was solved on screen or on paper? From personal experience, there’s a huge difference between, say, drawing a Slitherlink line on paper and drawing one in Paint or another image-editing program.
Your analysis of this battleship puzzle is wonderfully clear and educational. As you note, the ability to place both battleships and cruisers as a group is an extremely powerful technique. In Fathom It! terminology, ships of sequential sizes taken as a group are referred to as “virtual ships“. In the puzzle above, taking battleships (4-segments) and cruisers (3-segments) as a group results in “virtual cruisers”.
Often, after placing the battleship, the technique of placing “virtual destroyers” consisting of the remaining destroyers and cruisers can greatly simplify the solution.
It is conceivable that a puzzle could be best solved by placing “virtual destroyers” consisting of destroyers, cruisers, and battleships, but I have yet to come across a puzzle utilizing such a technique. It would be interesting to encounter a battleship puzzle that can be solved easily in this fashion.
Your comment that “whenever the big rows are next to each other (as in R1 and R2), you will most often find that you cannot use both of them simultaneously” is another extremely valuable technique obviously borne out of much experience with solving Battleship puzzles. I’m sure others will join me in thanking you for taking the time to share your solving insights.
Thanks for the comments Moshe. My recent puzzle #94 is pretty close to being a virtual destroyers puzzle — at least the logical conclusion I made in making it had to do with how to fit six large ships in the grid, but you do need to consider longer ships than just 2 unit ships in doing it. Most solvers reported guessing or using uniqueness, probably because thinking of 6 ships at one time is not a very common technique. But it has such an odd column distribution it might be nice to explore it again in another setting.