Dr. Sudoku Prescribes #47 – Battleships
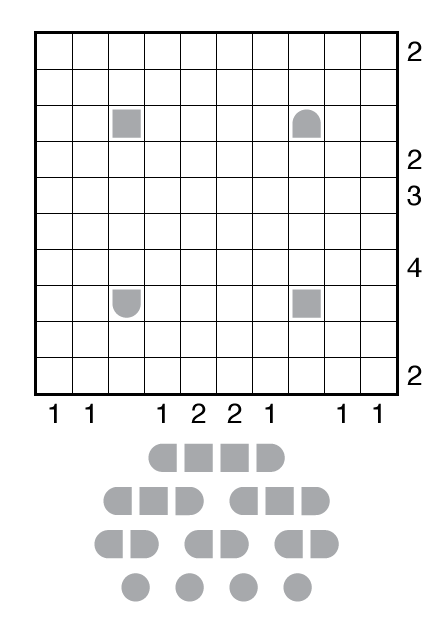
or solve online (using our beta test of Penpa-Edit tools; use tab to alternate between ship placement and shading modes. In ship placement mode, right click gives sea, left click gives circle/square, left click and drag for rounded ships.)
Theme: The Bermuda Quadrangle? The missing radar clues will complicate the solve.
Rules: Standard Battleships rules.
Answer String: For each row from top to bottom, enter the number of the first column from the left where a ship segment appears. If the row is empty, enter 0. Enter these numbers as a single string with no separators.
Time Standard: Battleships Grandmaster = 3:45, Master = 7:00, Expert = 14:00
Solution: PDF
Note: Advice on solving this puzzle has now been posted in “Ask Dr. Sudoku #8“

Nice use of counting up what the numbers on the left and bottom don’t account for. Wasn’t timing, but it was somewhere between 7 and 14.
>> Nice use of counting up what the numbers on the left and bottom don’t account for.
Yep, I liked that a lot.
Err, make that right and bottom.
1:45 , a little surprised with your estimate.Possibly overrated? I saw some standard deductions(the ‘4’ clue in the 7th row and the rounded segment in the 3rd row) for the break-in,to deduce the correct location of the 4-seg ship instantly.
I don’t see how you can deduce the location of the 4 ship without:
a) Figuring out that the top left middle given must go horizontal, because if it went vertical, then the two unclued columns would add to 10 and leave no room for a 4.
b) Realizing that after placing known ship parts to the left and right of the top-left middle given, you have the max number of placed parts in the unclued rows, allowing you to mark every other square in those rows.
Did you do something different that allowed you to place the 4 earlier?
The fact that the top-left has to be horizontal occured instantly to me based on the arithmetic.
The 4-seg ship had only two possible places : 8th col( I placed it first there) and the other one on the bottom-left given. I got lucky with placing the first ship. I would not know which one was correct before I would have reached a conflict. In this case,I found the correct placement,so the estimated times seem okay.
If “the fact that the top-left has to be horizontal occured instantly to me based on arithmetic” is true, that is why you solved the puzzle so fast. I do not believe that deduction is trivial and none of my test-solvers get there that fast either … certainly not “instantly”. It definitely can be done by leveraging the potential 4 locations with the total sum, but is a bit non-standard way to look at the puzzle in my opinion.
I did exactly what Scott mentioned and I wouldn’t call it standard, instant or trivial. It was quickly clear to me though that because of the locations of the 4 given ship segments, the key of the solve lay in the unclued rows, instead of the clued rows. So the first thing I did was calculate the unclued totals.
You can definitely get the top left horizontal somewhat quickly, but for me it was more like: bottom right is vertical by basic math; therefore submarines up top; vertical in top left would imply more submarines in the bottom, which would leave the 1 on the far left column hanging. I can see getting all of that really quickly, mind you since it’s basically the same deduction twice in a row with symmetry.
Yes. This is exactly how I intended it to be spotted; obviously I can’t force you to follow the path. You place 2 subs on the right (and know where one more must go). By symmetry column 3 does something different as you can’t put two more subs in the bottom row.
4hrs 48mins
Thnks for the helpful comments!for the first 3-4 hours i just placed only the 2 submarines at the top row and deduced that the top left segment has to be horizontal.Then i was clueless.
Went through the comments and got the idea that adding the segments in all the rows should equal 20 and all columns equal 20.Never used this logic at all.
Makes me remember the wonderful object placement star battle puzzle where this similar concept was used.
Beautiful puzzle motris!!Thnks
Counting to 20 was also an easy way to help break into the Sudoku from Thursday. The given numbers at the bottom add up to 16 there, which when combined with the four submarines is all 20. Therefore the remaining two columns are empty.
In general, placing the big ships and counting to twenty are almost always worth considering as ways to get into a puzzle. The fact that on Thursday and Friday the submarines got locked down early on and pushed the logic throughout is more unusual (and is one reason those puzzles were fun/memorable).
Yes, knowing the total ship count is always valuable in missing clue puzzles. I gave that suggestion yesterday when you asked for a hint on Thursday’s puzzle; I was hopeful you would have read it before attempting this one. But I’m glad you are starting to learn more tricks about Battleships.
I learned a lot while struggling through the challenges here, so thanks!
There’s definitely a lot more talk about counting here in the comments than I used in my solution. (Counting has become quite natural to me for Star Battle, but not previously for Battleship—it may be that most of the Battleship puzzles I’ve solved previously had all clues given.)
So next time, I’ll hope to use counting when appropriate and speed things up considerably.