Statue Park (Yajisan-Kazusan) by Jamie Hargrove
or solve online (using our beta test of Penpa-Edit tools)
Theme: Clue Symmetry & Logic
Author/Opus: This is the 6th puzzle from guest contributor Jamie Hargrove.
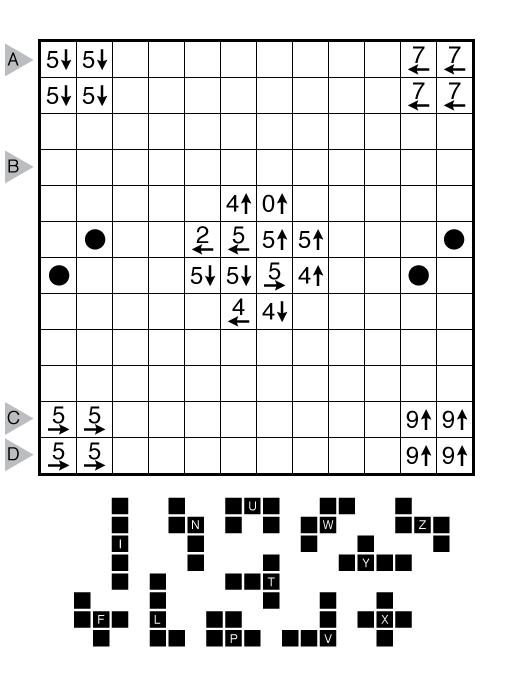
Rules: Place each of the twelve pentominoes into the grid once, with rotations and reflections allowed. No two pentominoes can overlap or be orthogonally adjacent, and all cells not occupied by the pentominoes must be orthogonally connected. The black circles indicate some cells that must be covered by pentominoes. Some numbers and arrows are also given in the grid. For all numbers that are not covered by a pentomino, the clues give the exact count of shaded cells in the given direction. A shaded over clue may or may not be true.
Answer String: Enter the length in cells of each of the shaded segments from left to right for the marked rows, starting at the top. Separate each row’s entry from the next with a comma.
Time Standards (highlight to view): Grandmaster = 10:30, Master = 17:15, Expert = 34:30
Solution: PDF
Note: Follow this link for other Statue Park Puzzles and this link for other less common Shading puzzles including Yajisan Kazusan puzzles.

Just wanted to comment that I really enjoyed this week of puzzles by Jamie. There were some unique puzzle styles that were well highlighted by their narrow solving paths.
Hey there. Great puzzle but I am stuck. I can’t figure out what pentominoes go in the center that will allow only one 5 to go uncovered without a uncovered 4 right next to it which would be a contradiction. Perhaps I am missing something here. Are some of the clues to be ignored. Also do all of the four black circles have to be covered by pentominoes? Thanks again for a create puzzle.
Cheers – Eugene
Hi Eugene — sounds like you are searching for the exact right thing (one 5 to go uncovered without any 4’s that cause contradiction). You may have overlooked the spot where this is possible, but it is how I got started when solving the puzzle.
Also, all black circles will be covered by a pentomino. (A pentomino may include more than one black circle.)
This puzzle had a very nice beginning with very clear logic that was very satisfying to find. Unfortunately that was it. After that break-in I could not find any further logical deduction that did not require massive checking of lots of possibilities. Finishing this felt like work. One of those rare puzzles on this blog where I wonder if there is some elegant path I comletely missed, or if it is supposed to be a more intuitive fiddly solve. Well, not every puzzle is for everyone, I guess.