Round Trip by Craig Kasper
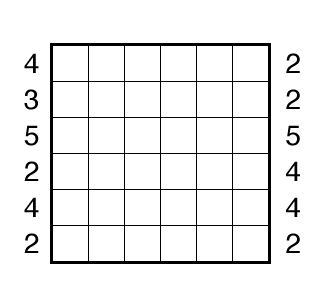
or solve online (using our beta test of Penpa-Edit tools; in default linex mode: left-click+drag draws line, right click marks X on edge)
Theme: Taking Sides
Author/Opus: This is the 5th puzzle from guest contributor Craig Kasper.
Rules: Draw a single loop in the grid which may cross itself orthogonally, but otherwise does not touch or retrace itself. The clue numbers to the left/right of the rows indicate the number of squares visited by the nearest section of the loop that travels horizontally in the rows. The clue numbers to the top/bottom of the columns indicate the number of squares visited by the nearest section of the loop that travels vertically in the columns.
Also, see this example:
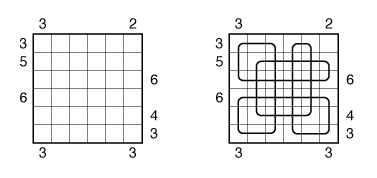
Answer String: Enter the number of empty squares for each row from top to bottom, followed by a comma, and then the number of turns for each row from top to bottom. This example has the key “100000,422224”.
Time Standards (highlight to view): Grandmaster = 0:40, Master = 1:30, Expert = 3:00
Solution: PDF
Note: Follow this link for other Round Trip puzzles. Some more Round Trip puzzles can be found in the book Loop Variety Collection by Ashish Kumar and Murat Can Tonta.

A few preliminary thoughts on the new genre.
There’s a bit of something like CTS or Coral (or Paint by Numbers etc) at the start where you try to draw some segments to satisfy the clues. After that, the loop logic gets pretty interesting, and I like the way you have to think about loop logic to piece it together. The possibility of blank squares definitely boosts the challenge a bit since you can’t just fill stuff in on auto-pilot the way you often can where every square must be visited.
Interesting puzzle type. Looking forward to more of these I think.
That said, I found that when I had completed the top two thirds of the puzzle the last 2 lines came to me more intuitively than logically, and for a few moments after I finished I found myself looking for other possible solutions…
– Neelix
Oh a new type, so I looked at the example first.
Interesting, we must construct a loop that can cross itself but must always turn in the same direction (e.g. right) at every corner…