Nanro by Prasanna Seshadri
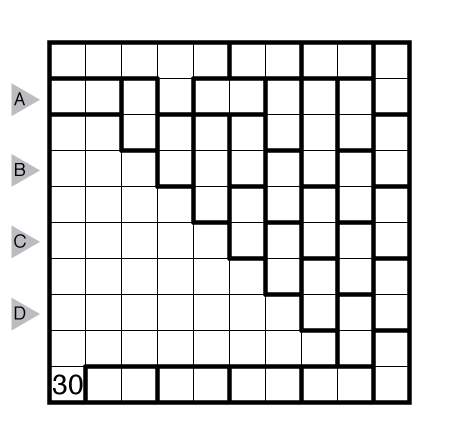
or solve online (using our beta test of Penpa-Edit tools; use the tab key to alternate between shading and number entry modes)
Theme: No Extra Numbers
Author/Opus: This is the 19th puzzle from our contributing puzzlemaster Prasanna Seshadri.
Answer String: Enter the length in cells of each of the segments labeled with numbers from left to right for the marked rows, starting at the top. Separate each row’s entry from the next with a comma.
Time Standards (highlight to view): Grandmaster = 2:45, Master = 5:00, Expert = 10:00
Solution: PDF
Note: Click here for other Nanro puzzles. If you are new to this puzzle type, please first try out the example on the Rules and Info page as well as this easy Nanro post.

02:55
This theme is impressive. And after the obvious, it’s still dang hard with all the possible 1’s and 2’s. Nicely done.
Looking at the puzzle, I was expecting more of an intuitive solve than a deductive one, but the deductive path (once I found it) ended up working better. Curious if anyone else had the same experience.
Truly beautiful puzzle. I haven’t seen anything like this.
I really liked this one – and I appreciate the gentle background theme of pushing something to an extreme that seems to relate most of the puzzles this week.
My first feeling was that there had to be a simple way to fill the 30, and that the puzzle would be unsolvable otherwise. Does that count as an intuitive solve? 🙂
If you didn’t prove it rigorously then yes, it’s intuitive. But you can use the fact that there are at most three “black cells” (numbers) in a 2×2 square, and apply that to the big region for a rigorous proof. (I spent like 20-30 seconds for this.)
True enough — the fill-in for the 30-block was forced either way. When I made my comment above re intuitive vs deductive, I had the smaller blocks in mind.
That was fun ! I’ve proven the 30 like this :
Gur 30 ertvba pbagnvaf 36 pryyf fb 6 bs gurz fubhyq or hahfrq. Guvf ertvba pbhyq pbagnva 21 bireynccvat 2k2 fdhnerf bs juvpu 6 pbhyq pbrkvfg jvgubhg bireync yrnivat 12 pryyf va gung ertvba bhgfvqr bs gubfr 6 2k2 fdhnerf. Gung zrnaf gung va rnpu bs gubfr 6 2k2 fdhnerf 1 pryy vf hahfrq naq gur erznvavat 6*3+12 pryyf zhfg or hfrq. Lbh pbhyq ercrng gung sbe qvssrerag 6 fdhnerf bhg bs gur 21 cbffvovyvgvrf gb sbepr nabgure frg bs 12 hfrq pryyf. Gung yrnqf dhvpxyl gb 3 hfrq pryyf va n fdhner fb gur 6 hahfrq pryyf pbhyq rnfvyl or qrsvarq.
Guess I’m not as fancy in QED as you guys, but reading these I guess I did this correctly. I counted 36 squares of which 30 had to be filled in, and knowing the 2×2 rule I noticed there was only gonna be one way to stuff in all those shaded squares.